Euler-Bernoulli梁とTimoshenko梁のビーム要素、フレーム要素の定式化と計算結果比較
1. はじめに
前記事で1次元構造要素のトラス、ビーム、フレーム要素によるFEM変位計算を行いましたが、そこで用いたビーム、フレームはEuler-Bernoulli梁をもとにしていました。
本記事ではTimoshenko梁のビーム、フレーム要素を用いて計算しています。
2.Euler-Bernoulli梁とTimoshenko梁
Euler-Bernoulli梁では、
(1)断面は変形しない
(2)変形前の中立軸に垂直な断面は、変形後の中心軸に垂直な平面を保つ
Timoshenko梁では、上の仮定でなく、
(1)断面は変形しない
(2)変形前の中立軸に垂直な断面は、変形後も平面を保つ
Euler-Bernoulli梁

Timoshenko梁

FEMによる定式化をpdfにまとめました。
トラス、ビーム、フレーム要素(Euler-Bernoulli)
Truss, Beam and Frame Elements
http://starlightparade.usamimi.info/ivyfem/doc/TrussBeamFrame.pdf?p=0
Timoshenko梁
Timoshenko Beam and Frame Elements
http://starlightparade.usamimi.info/ivyfem/doc/TimoshenkoBeamFrame.pdf?p=0
3. 梁の曲げ

棒の断面(y-z面)は、
b=0.2 m
h = (1/4)b
材料定数は、
E=169 GPa
ν=0.262
ρ=2300 kg/m^3
bの方向軸(y軸)の断面2次モーメントは、
Iz=(1/12) b h^3
棒の軸方向(x軸)の断面2次(極)モーメントは、
Ix =(1/12) b h^3 + (1/12) b^3 h
とします。
片持ち梁の荷重(断面力)は、
Fy = -0.5 x 10^6 [N m^2]
とします。
3.1. Euler-Bernoulliビーム要素
フレーム要素と同等の結果でした。
3.2. Euler-Bernoulliフレーム要素
Fy = -0.5 x 10^6 [N m^2]

3.3. Timoshenkoビーム要素
Fy = -0.5 x 10^6 [N m^2]

3.4. Timoshenkoフレーム要素
Fy = -0.5 x 10^6 [N m^2]

4.トラス付きの梁
トラスの一辺L=1m、したがって梁の長さは2Lになります。一辺Lにつきフレーム要素で10分割しています。
棒の断面は、
b=0.2 m
h = (1/4)b
材料定数は、
E=169 GPa
ν=0.262
ρ=2300 kg/m^3
bの方向軸の断面の2次モーメントは、
I=(1/12) b h^3
とします。

4.1. Euler-Bernoulli梁のフレーム要素

4.2. Timoshenko梁フレーム要素

5.まとめ
梁理論としてEuler-Bernoulli梁とTimoshenko梁を用いてFEM定式化しました。片持ち梁、トラス付き梁について計算しました。
両端支持梁の固有振動のFEM固有値計算(ビーム要素、フレーム要素、線形弾性体、Saint Venant超弾性体)
1. はじめに
ビーム要素とフレーム要素を実装したので、両端支持梁の固有振動を計算しました。
比較するために線形弾性体、Saint Venant超弾性体でも固有振動を計算しています。
2.両端支持梁

棒の断面は、
b=0.2 m
h = (1/4)b
材料定数は、
E=169 GPa
ν=0.262
ρ=2300 kg/m^3
bの方向軸の断面の2次モーメントは、
I=(1/12) b h^3
とします。
3. ビーム要素
フレーム要素と同等の結果が得られました。
4. フレーム要素

規格化周波数b/λ = 2.93 x10^(-7)
5.線形弾性体

規格化周波数b/λ = 5.39×10^(-7)
6.Saint Venant超弾性体

規格化周波数b/λ = 5.39×10^(-7)
7. 以上から
線形弾性体、Saint Venant超弾性体でも自由周波数を計算すると、フレーム要素の桁と一致することが分かります。
ちなみに、理論計算すると、
ω = (π/l)^2 √(EI/(ρA)) = 1.29 x 10^(-7)
でやはり桁は一致しています。
8.まとめ
ビーム要素、フレーム要素、線形弾性体、Saint Venant超弾性体を用いて固有振動を計算しました。
梁要素(トラス、ビーム、フレーム)を用いたFEM構造計算
1. はじめに
円柱や角柱のような棒をつなげて構造物を作るとき、柱の断面が長手方向に比べて十分小さい場合は、1次元の梁理論が適用できます。
弾性体を三角形要素で分割して曲げなどを計算しましたが、梁要素を使えば1次元として扱うことができ、線要素で分割することになります。
今回、梁要素として、軸方向の変位のみがあるトラス要素、一方向の軸に垂直な方向のたわみと回転を扱えるビーム要素、複数方向の梁を組み合わせることができるフレーム要素(トラス要素とビーム要素の足し合わせ)を実装しました。
2. トラス要素
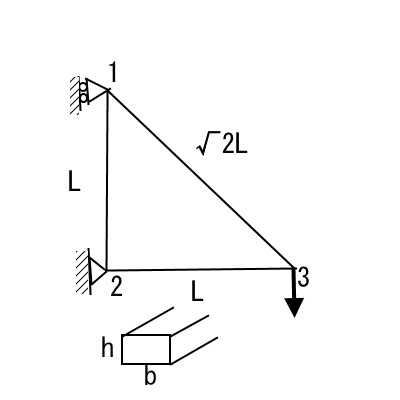
棒の断面は、
b=0.2 m
h = (1/4)b
材料定数は、
E=169 GPa
ν=0.262
ρ=2300 kg/m^3
bの方向軸の断面の2次モーメントは、
I=(1/12) b h^3
とします。
トラス要素は1つの辺に1つだけ割り当てました。(計3要素)
計算結果

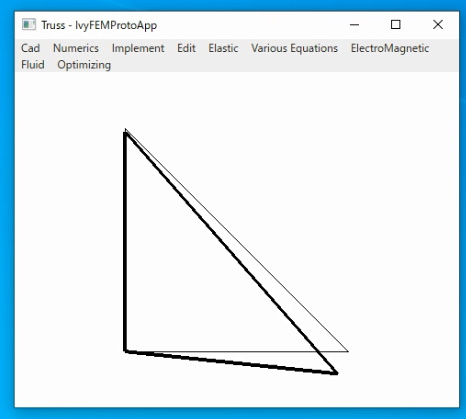

点1はローラーなので垂直方向に上下することが計算結果よりわかります。
3.ビーム要素(一方向)
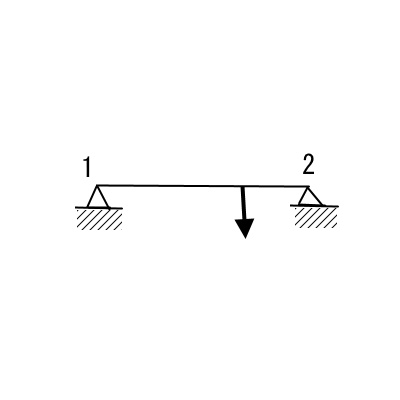
梁の長さL=1mです。
ビーム要素で10分割しています。すべてのビーム要素が一方向に向いている場合のみ適用可能です。
計算結果

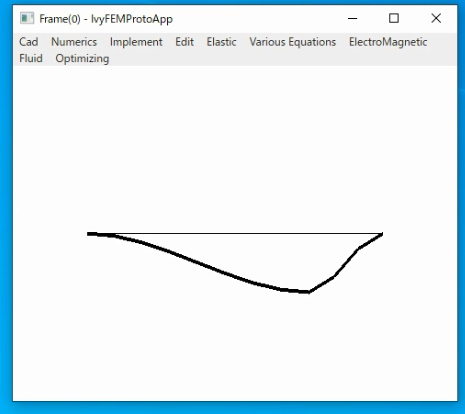

4. フレーム要素
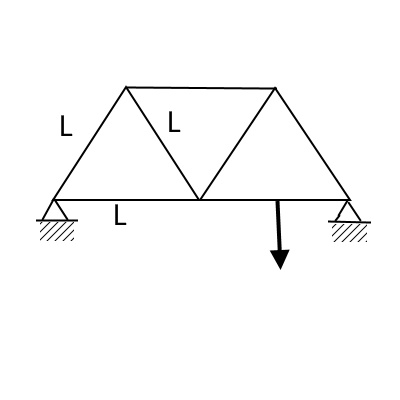
梁にトラスを付けた構造を計算しました。トラス要素とビーム要素の両方をあわせたフレーム要素を用います。
トラスの一辺L=1m、したがって梁の長さは2Lになります。一辺Lにつきフレーム要素で10分割しています。
計算結果



5.まとめ
トラス、ビーム、フレーム要素を用いて骨組構造の計算を行いました。
なお、ここではEuler-Bernoulliの梁理論を使いました。他の方法もあるようなのでまたの機会に。
開放形導波路(Open-type, unbounded waveguides)のベクトル波固有モード計算
1. はじめに
前に遮蔽形導波路のベクトル波固有モードをedge/nodal FEMを用いて計算しました。
今回は遮蔽ボックスを取り払った場合、つまり開放形(Open-type, unbounded)の導波路をFEMを用いて計算しています。
開放形導波路の場合は、無限領域を内部の有限領域に限定し、領域の境界積分項を評価する必要があります。ここでは、外部領域では指数関数減衰するとして定式化しています。
2. 開放形導波路の固有モード解析の定式化
pdfにまとめました。
http://starlightparade.usamimi.info/ivyfem/doc/EigenEdgeElementOpen.pdf?p=0
3. 開放形異方性導波路の固有モード計算結果
コアの高さh、コアの幅s
s = 2 h
領域の幅W、領域の高さH
H = 0.75 * W
h = (1.0 / 2.0) * H
コアの比誘電率
εxx = 2.31
εyy = 2.19
εzz = 2.31
クラッドの比誘電率
εcladding = 2.05
計算には電界Eを用い、基本モードを計算しました。







4.開放形マイクロストリップ線路の固有モードの計算
ストリップ線路の幅s、基盤の高さh
s = 2 h
領域の幅W、高さH
H = (2.0 / 4.0) * W
h= (1.0 / 4.0) * W
基盤の比誘電率 εboard = 2.55
空気の比誘電率 εvacuum= 1.0
計算には電界Eを用い、基本モードを計算しました。









5.まとめ
開放形導波路のベクトル波固有モードを、edge/nodal FEMに外部領域の減衰波を表す境界積分項を加えることで計算できるようにしました。
Vorticity Equationsによる流体のFEM計算ー標準ガラーキン法(Newmark βとRK4)とSUPG(streamline upwind Petrov-Galerkin)
1. はじめに
Navier-Stokes方程式は速度ベクトルvと静水圧pを解く方程式でしたが、対流を表すvorticityベクトル ωと流線を表すstream functionベクトル ψを用いた定式化もできます。
2次元問題の場合、vorticity、stream functionは1方向しか成分を持たないので、2成分解析が可能です。
本記事では、Vorticity Equationsの導出と弱形式の導出、直接解法とRK4解法、さらにkinematic viscosity νが小さい場合の計算のためにSUPG(streamline upwind Petrov-Galerkin)を用いた定式化について記します。
Vorticity Equationsを用いた定式化では、境界条件がわからず、いろいろ試しました。なんとかうまくいった方法を示しています。
2. Vorticity Equationsの定式化ー標準ガラーキン法(直接法とRK4)とSUPG
pdfにまとめました。
Vorticity Equations of Navier-Stokes Equations - Standard Galerkin and SUPG Formulations -
http://starlightparade.usamimi.info/ivyfem/doc/VorticityStdGSUPG.pdf?p=0
3. Vorticity Equations:標準ガラーキン法(Newmark β)
3.1. lid driven cavity(時間領域)
一辺の長さ1[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.02
ベクトルは速度ベクトルを表し、サーモグラフィーはvorticityを表しています。




3.2. Back-step(時間領域)
入力(左側)の幅0.3[m]、出力(右側)の幅1.0[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.02




4.Vorticity Equations:標準ガラーキン法 + RK4(4次Runge-Kutta)
RK4では
時間刻み幅⊿tが大きいと発散するのでかなり細かく刻んでいます。
4.1. lid driven cavity(時間領域)
一辺の長さ1[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.02








5. SUPG(Newmark β)
粘性率を小さくした場合の計算結果です。
5.1. lid driven cavity(時間領域)
一辺の長さ1[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.0002




5.2. Back-step(時間領域)
入力(左側)の幅0.3[m]、出力(右側)の幅1.0[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.0002











6. まとめ
VorticityとStream functionを用いた流体の支配方程式を導き、弱形式を求めた。
詳細はpdfに記したが境界条件で苦労した。
標準ガラーキン法の場合は、Newmark β法とRK4で計算した。
SUPGの場合はNewmark β法で計算した。
Vorticity Equationsによる流体のFEM計算ー標準ガラーキン法(Newmark βとRK4)とSUPG(streamline upwind Petrov-Galerkin)
1. はじめに
Navier-Stokes方程式は速度ベクトルvと静水圧pを解く方程式でしたが、対流を表すvorticityベクトル ωと流線を表すstream functionベクトル ψを用いた定式化もできます。
2次元問題の場合、vorticity、stream functionは1方向しか成分を持たないので、2成分解析が可能です。
本記事では、Vorticity Equationsの導出と弱形式の導出、直接解法とRK4解法、さらにkinematic viscosity νが小さい場合の計算のためにSUPG(streamline upwind Petrov-Galerkin)を用いた定式化について記します。
Vorticity Equationsを用いた定式化では、境界条件がわからず、いろいろ試しました。なんとかうまくいった方法を示しています。
2. Vorticity Equationsの定式化ー標準ガラーキン法(直接法とRK4)とSUPG
pdfにまとめました。
Vorticity Equations of Navier-Stokes Equations - Standard Galerkin and SUPG Formulations -
http://starlightparade.usamimi.info/ivyfem/doc/VorticityStdGSUPG.pdf?p=0
3. Vorticity Equations:標準ガラーキン法(Newmark β)
3.1. lid driven cavity(時間領域)
一辺の長さ1[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.02
ベクトルは速度ベクトルを表し、サーモグラフィーはvorticityを表しています。




3.2. Back-step(時間領域)
入力(左側)の幅0.3[m]、出力(右側)の幅1.0[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.02




4.Vorticity Equations:標準ガラーキン法 + RK4(4次Runge-Kutta)
RK4では
時間刻み幅⊿tが大きいと発散するのでかなり細かく刻んでいます。
4.1. lid driven cavity(時間領域)
一辺の長さ1[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.02








5. SUPG(Newmark β)
粘性率を小さくした場合の計算結果です。
5.1. lid driven cavity(時間領域)
一辺の長さ1[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.0002




5.2. Back-step(時間領域)
入力(左側)の幅0.3[m]、出力(右側)の幅1.0[m]
密度ρ = 1.2[kg/m^3]
粘性率μ = 0.0002











6. まとめ
VorticityとStream functionを用いた流体の支配方程式を導き、弱形式を求めた。
詳細はpdfに記したが境界条件で苦労した。
標準ガラーキン法の場合は、Newmark β法とRK4で計算した。
SUPGの場合はNewmark β法で計算した。
流体力学の支配方程式(Navier-Stokes Equations)を導く
流体力学の支配方程式、Navier-Stokes方程式を導く過程をpdfにまとめました。
以下の順に説明しています。
3 時間導関数
4 Eular の膨張公式
5 Reynolds の輸送定理
6 連続の式
7 Cauchy の第一運動法則
8 Cauchy の第二運動法則
9 非圧縮性の式
10 流体の構成式
11 Stokes 流体
12 Newton 流体
13 Navier-Stokes の方程式
http://starlightparade.usamimi.info/ivyfem/doc/FluidDynamicsNavierStokes.pdf?p=0