1. はじめに
薄板の曲げの理論にはKirchhoffの板理論があります。ただ、この理論に基づく2次元要素に有効なものはないとのことです。
Kirchhoffの板理論を一般化したReissner-Mindlinの板理論を基礎とし、2次三角形要素の6節点上でのみKirchhoffの仮定を満たすとしたDiscrete Kirchhoff Theory(DKT)は有効な要素であることが知られています。
〇Kirchhoffの板理論
変形前中立面に垂直だった直線は変形後も直線であり、その直線は変形後の中立面に垂直である
〇Reissner-Mindlinの板理論
変形前中立面に垂直だった直線は変形後も直線であるが、その直線は変形後の中立面に垂直である必要はない
2. 定式化
pdfにまとめました。
Plate Bending Theory of Discrete Kirchhoff Triangle (DKT) Elements
http://starlightparade.usamimi.info/ivyfem/doc/DKTPlate.pdf?p=0

3. 計算結果
3.1. 曲げの計算結果

板の寸法
a = 1.0
b = a
厚さh = 0.2a
板の材料定数
密度ρ = 2.3 x 10^+3 kg/m^3
Young率 E = 169.0 x 10^+9
Poisson比 = 0.262
せん断補正係数Ks = 5.0 / 6.0(長方形断面)
3隅を固定し、残りの1隅に垂直方向の荷重をかけたとき


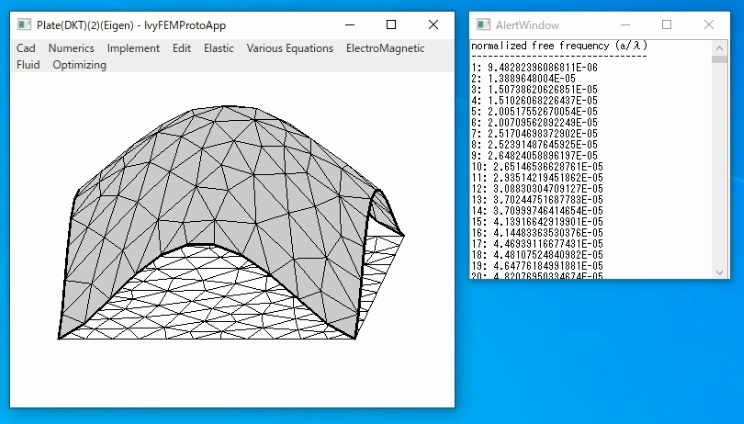
3.2. 固有振動(固有値問題)
3隅を固定したとき、

4隅を固定したとき、
4.まとめ
Discrete Kirchhoff理論に基づく薄板三角形要素を実装し、曲げの計算を行いました。