1. はじめに
幾何学的非線形梁をTotal Lagrange法を用いて計算します。
Euler-Bernoulli梁の場合は、変位と回転角に関係式が存在するため、変位2つ(uX、uY)と回転角(θ)は自由度について非線形な補間関数を構成する必要があります。これをfield-consistentな補間と呼んでいます。
Timoshenko梁の場合は、変位uX、uYとθは独立して補間、つまり従来のLagrange補間しても問題ないようです。
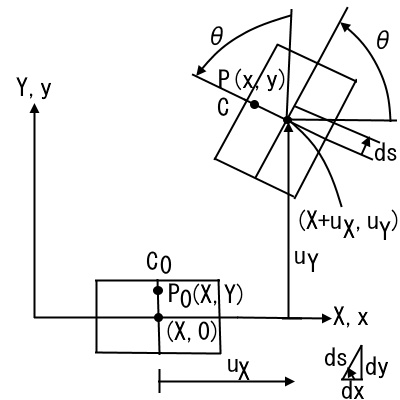
2. Total Lagrangian Beamの定式化
pdfにまとめました。
Euler-Bernoulli Field-Consistent Beam(Frame) Using Total
Lagrangian Formulation
http://starlightparade.usamimi.info/ivyfem/doc/FieldConsistentTLFrame.pdf?p=0
Timoshenko Beam(Frame) Using Total Lagrangian Formulation
http://starlightparade.usamimi.info/ivyfem/doc/TimoshenkoTLFrame.pdf?p=0
3. 片持ち梁の計算結果
梁
長さL = 1m
幅b = 0.2L
高さh = 0.25b
梁の物性値
密度ρ = 2.3e+3 kg
Young率 E = 169.0e+9
Poisson ν= 0.262
とします。
FはY方向荷重で、上方向を+とします。
以下の結果のグラフでuはX方向(水平方向)変位、vはY方向(垂直方向)変位です。
mは断面換算の荷重で、断面積A(=bh)として、
m = F A = F (bh) [kg m^2]
としています。

3.1. Euler-Bernoulli field-consistent Beam


3.2. Timoshenko Beam
shear locking回避のため剛性行列の計算には低減積分を用います。


4. まとめ
幾何学的非線形な梁を扱うためにTotal Lagrange法を導入しました。
Euler-Bernoulli梁の場合は、field-consistentな補間関数を構成する必要性が分かりました。Timoshenko梁の場合は、従来の補間関数を用いることができることを確認しました。