弾性波プレート導波路(elastic plate waveguides)、Lamb waveの伝達問題(不連続問題、散乱問題）

1. はじめに

弾性波プレート導波路を伝搬するLamb waveの基本モードをポート1から入射したとき、不連続部により反射する、またはポート2に透過するのをFEMで計算しています。

基本モードは対称な分布のモードのため、中央面(mid-plane)を境に半分にした領域で計算できます。

2. 弾性波プレート導波路、Lamb waveの伝達問題の定式化

pdfにまとめました。

Frequency Domain FEM Formulations for Lamb Wave Elastic
Plate Waveguides – Eigenvalue Problem and Discontinuity
Problem

http://starlightparade.usamimi.info/ivyfem/doc/ElasticLambWaveguide.pdf?p=0

3. 計算結果

ポアソン比ν=0.31とします。ヤング率Eや密度ρは反射、透過特性には無関係なので、E=1、ρ=1としておきます。

導波路に亀裂が入ったときの反射、透過特性を計算しました。

入出力導波路の固有モードも（解析解でなく）FEMで計算してます。

図は導波路をmid-planeで半分にしたものです。

導波路幅をWとすると、図の幅d=W/2になります。

亀裂の深さhは、h/d = 0.8としています。

また亀裂の角度は2θ=10°としています。

下記文献を参照してください。

Masanori Koshiba, Shoji Karakida, and Michio Suzuki, ”Finite-Element Analysis of Lamb Wave Scattering in an Elastic Plate Waveguide”, IEEE Transactions on Sonics and Ultrasonics, vol. su-31, no. 1,
January 1984

規格化周波数

fn = ksW/π

波数

ks=√(ρ/μ) 

不連続部の変位(displacement)ベクトル分布 Re(ux, -j uy)

入力導波路ポート1の反射係数|S11|、出力導波路ポート2の透過係数|S21|

入力導波路の固有モードの分散特性、分布

の計算結果は次のようになりました。

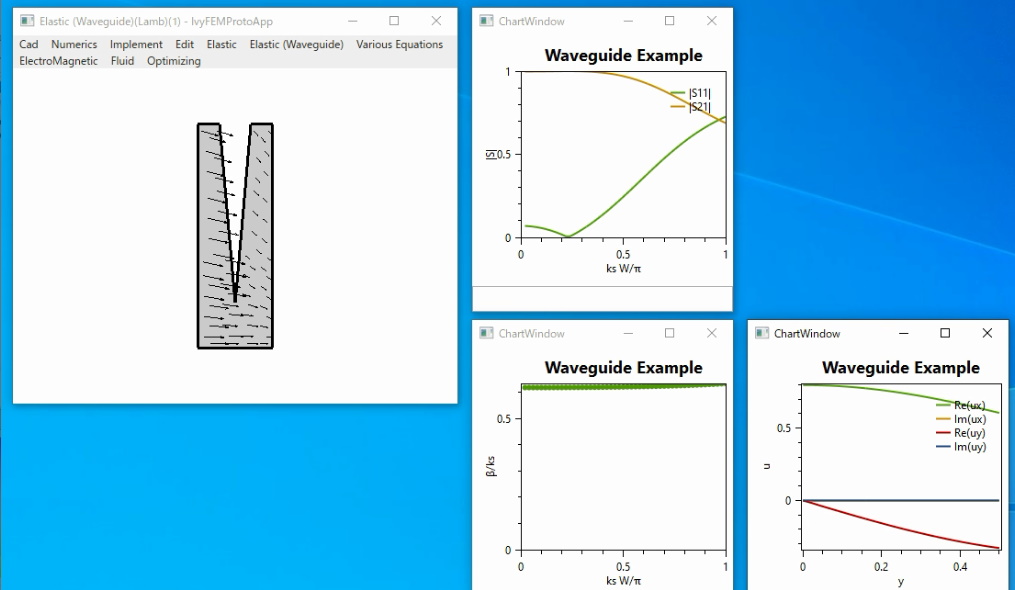
h/W=0.8のとき、fn=ksW/π=1で、反射係数|S11|=0.7になることが文献に載っています。今回の計算結果と一致しています。

また、h/W=0.5のときfn=1で|S11|=0.4になることが文献に載っていますがこれも計算したところ一致することを確認しました。

4. まとめ

弾性波プレート導波路の伝達問題をFEMで定式化し、導波路に亀裂が入ったときの反射、透過特性を計算しました。