FDTDによるH面誘電体装荷共振器のSパラメータの計算(3)
前回、前々回でSパラメータを計算するとき、以下の方法を試しました。
(1)入射波、反射波、透過波の到達する期間を切り出してFFTを掛ける。抽出期間(波形データの個数)は同じとする。
FDTDを試してみます(FDTDによるH面誘電体装荷共振器のSパラメータの計算)
http://ryujimiya.hatenablog.com/entry/2013/04/16/045609
(2)入射波(または反射波)として扱うときは反射波(または入射波)の到達する区間を0にする。透過波は全区間のデータを使用する。
FDTDによるH面誘電体装荷共振器のSパラメータの計算(2)
http://ryujimiya.hatenablog.com/entry/2013/04/17/004128
どちらもポート1の波形データを入射波と反射波に分離する際、分離する時刻の見極めが必要でした。
今回は、直線導波管で入射波を計算して、それを誘電体装荷共振器のポート1の界から引き算する方法をとってみました。シミュレーション回数は、直線導波管、誘電体装荷共振器の2回となりますが、FFTに関する調整がなくなるのでこちらの方がいいかもしれません。
入力導波管の長さd1 = 400 dxのとき
図面(比誘電率分布)
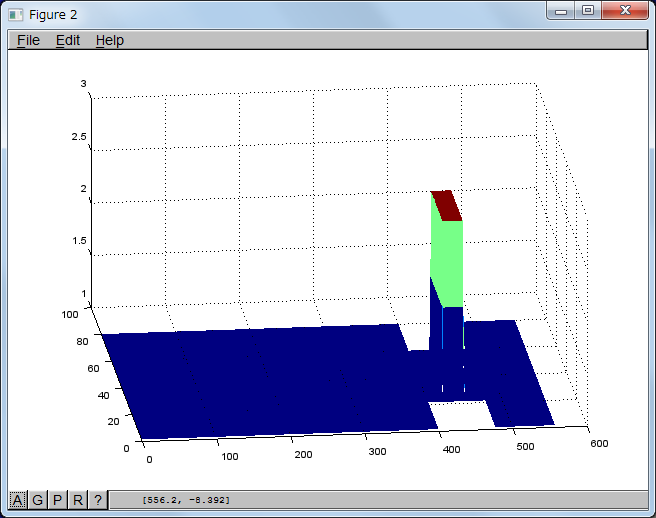
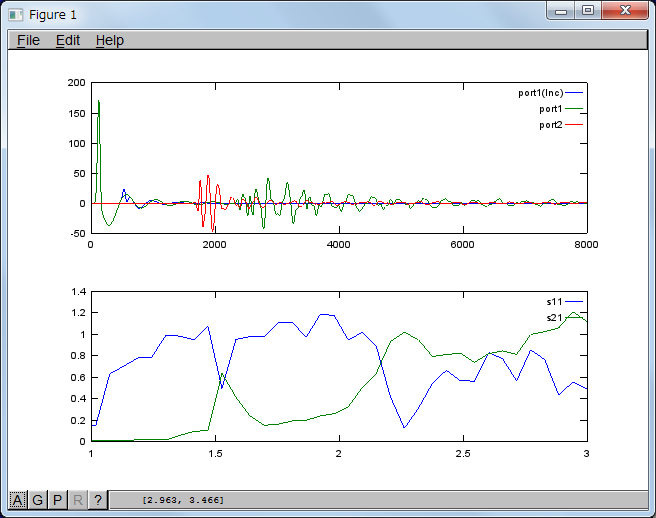
計算結果(素のガウシアンパルス)
入力導波管の長さd1 = 80 dxのとき
図面(比誘電率分布)
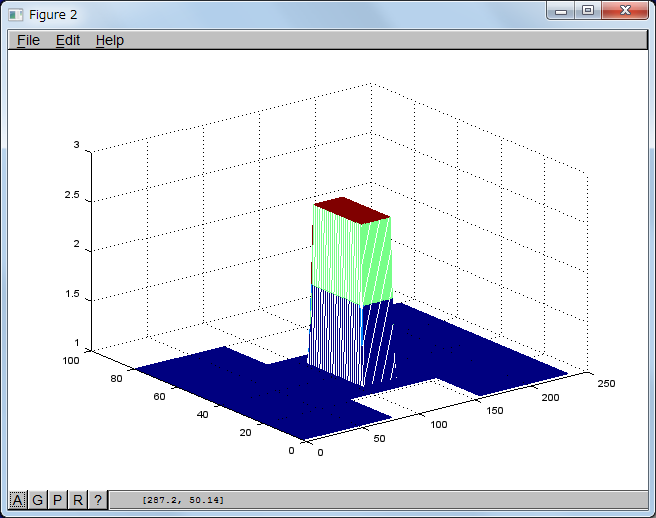
計算結果(素のガウシアンパルス)
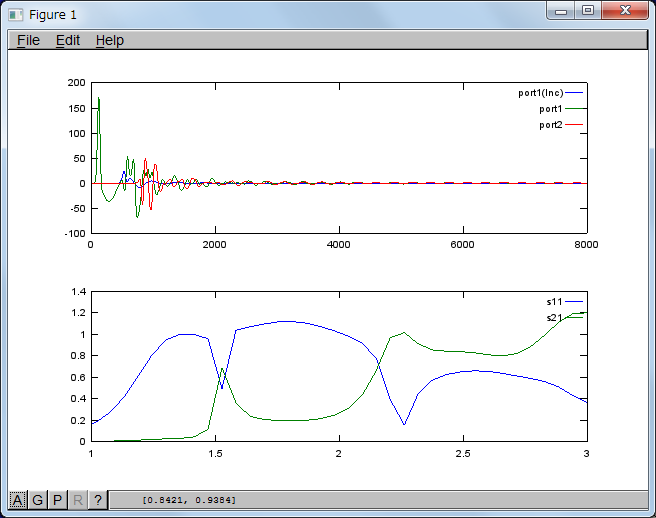
グラフの上半分は直線導波管のポート1上、誘電体装荷導波管のポート1、及びポート2の電界Ezの時間変化Ez(t)を示したものです。グラフの下半分が反射係数S11、透過係数S21の絶対値の周波数特性です。FEMの計算結果と比べると、まだ満足できる結果とは言えないですが、分割数が足りないからかもしれません。
今回の計算方法では、入射波の到達期間と反射波の到達期間が重なっていても問題ないので、d1 = 40 dx のとき正弦波変調ガウシアンパルスを入射させても反射係数を求めることができます。
搬送波規格化周波数fnc = 1.5 のとき
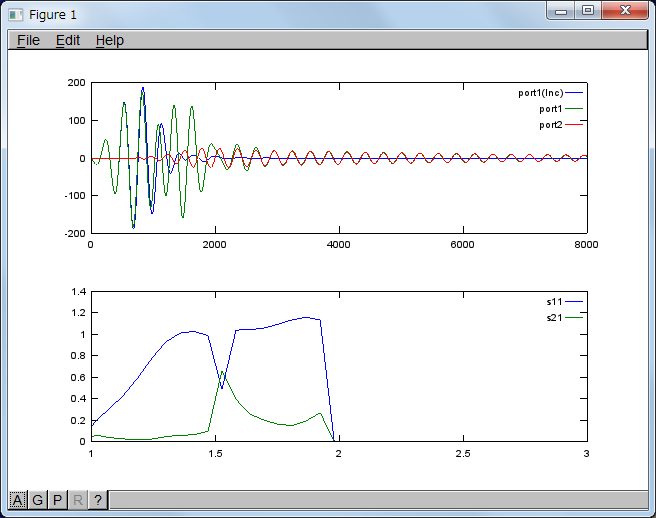
搬送波規格化周波数fnc = 2.5のとき
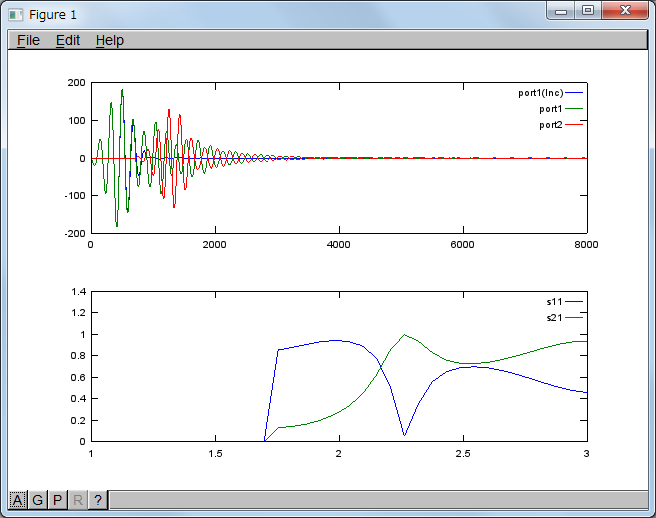
【追記(2013-04-20)】
入力導波管の長さd1 = 200 dxとし、計算ループ数を10000にしたときの結果
ガウシアンパルス励振時
Ez(t) = Ez(y) exp[ - (1/2) {(t - delay) / T}^2 ]
delay = 120 dt
T = 30 dt / √2
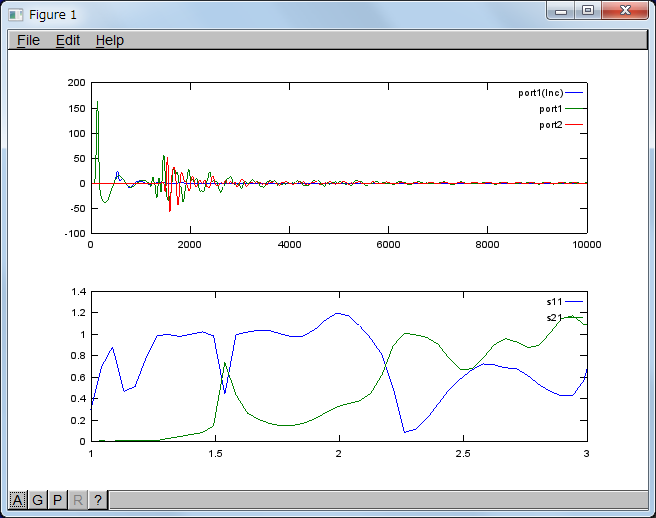
ガウシアンパルスの時間微分励振時
Ez(t) = Ez(y) { - √2・ (t - delay) / T } exp[ - (1/2) { (t - delay) / T }^2 ]
delay = 120 dt
T = 30 dt / √2
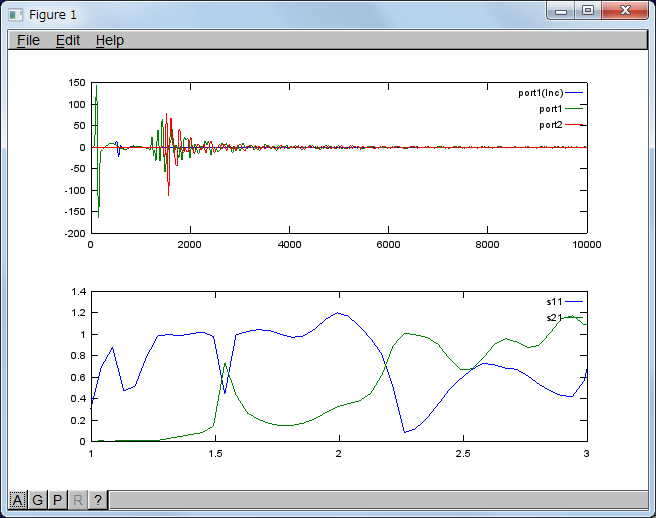
main_wg2d_problem01_2.m
https://gist.github.com/ryujimiya/5404802
wg2d_dielectric_filter.m
https://gist.github.com/ryujimiya/5396333
wg2d_straight.m
https://gist.github.com/ryujimiya/5404764