厚さの伸び縮みを考慮したMITC3シェル要素の定式化と非圧縮性超弾性体(Mooney-Rivlin)の薄板曲げ計算
1. はじめに
前記事ではMITC3シェル要素を用いた幾何学的非線形な変形の計算を行いました。
本記事では非圧縮性超弾性体(Mooney-Rivlinモデル)をMITC3シェル要素で解いています。
前記事ではSt.Venant-Kirchhoffモデルを用いましたが、厚さは変化しないものとして定式化しました。
非圧縮性超弾性体の場合は厚さの伸び縮み(thickness stretching)を考慮する必要があるため、定式化しなおしています。
2. 厚さの伸縮を考慮したMITC3定式化、非圧縮超弾性体の定式化
pdfにまとめました。
Thickness Stretching MITC3 Plate Formulation for Hyperelastic
Material (Moony-Rivlin Model)
http://starlightparade.usamimi.info/ivyfem/doc/MITCMooneyRivlinPlate.pdf?p=0
3. 計算結果
3.1. St.Venant-Kirchhoffモデル
まず厚さの伸縮を考慮したMITC3定式化の妥当性を確認するために、St.Venant-Kirchhoffモデルで計算しました。
板の寸法
a = 1.0
b = a
厚さh = 0.2a
板の材料定数
密度ρ = 2.3 x 10^+3 kg/m^3
Young率 E = 169.0 x 10^+9
Poisson比 = 0.262
せん断補正係数Ks = 1.0(使わない)



3.2. 超弾性体:Mooney-Rivlinモデル
素の主不変量を用いたMooney-Rivlinモデルの場合は収束しない結果となりました。
そこで、低減主不変量を用いたMooney-Rivlinモデルで計算しました。
非圧縮条件はLagrange未定乗数を用いて課しますが、平面応力場の条件を用いるとあらかじめLagrange未定乗数を求めることができ最終的に解く式にはラグランジュ未定乗数は現れません。
板の寸法
a = 1.0
b = a
厚さh = 0.2a
板の材料定数
Mooney-Rivlinの材料定数c1 = 1.0, c2 = 0.5



4.まとめ
超弾性体の薄板曲げを計算するためにMITC3の厚さの変化を考慮した定式化を用いました。
MITC3シェル要素を用いた線形弾性体及び幾何学的非線形(有限回転)(St.Venant-Kirchhoff)薄板の曲げ計算
1. はじめに
これまで薄板の曲げの計算にDKT(discrete Kirchhoff Theory)要素、Mindlin薄板要素を用いました。これらはKirchhoff-Love板理論やReisner-Mindlin板理論といった特別な仮定のもとで定式化したものです。
一方3次元のソリッド要素、例えば三角柱要素の高さhを0に近づけて三角形要素にするdegenerated要素があります。この方法では特別な板理論の仮定に依存しないので線形ひずみのみならず、幾何学的非線形弾性体にも適用可能となります。
degenerated要素には大きな欠点があり、shear lockingとよばれる実際より硬い不正確な解が得られます。これを解決する方法としてMITC(Mixed Interpolation of Tensorial Components)の手法です。MITC要素はdegenerated要素の定式化で、ひずみの補間を変更します。共変面内ひずみ成分はdegenerated要素の補間から導かれる式をそのまま使いますが、共変横せん断ひずみ成分だけ新たな補間を導入します。この共変横せん断ひずみをassumedひずみと呼んでいます。
本記事ではMITC3要素 (MITC3節点三角形要素)を用いた線形及び非線形な曲げ計算を行っています。
2. MITC3要素定式化
定式化をpdfにまとめました。
〇MITC3線形
Mixed Interpolation of Tensorial Components(MITC) Triangular
Elements for Linear Plate Bending
http://starlightparade.usamimi.info/ivyfem/doc/MITCLinearPlate.pdf?p=0
〇MITC3幾何学的非線形(St.Venant-Kirchhoffモデル)
Geometrically Nonlinear MITC3 Plate Formulation
(St.Venant-Kirchhorff Model)
http://starlightparade.usamimi.info/ivyfem/doc/MITCStVenantPlate.pdf?p=0


3.計算結果

板の寸法
a = 1.0
b = a
厚さh = 0.2a
板の材料定数
密度ρ = 2.3 x 10^+3 kg/m^3
Young率 E = 169.0 x 10^+9
Poisson比 = 0.262
せん断補正係数Ks = 1.0(使わない)
3隅を固定し、残りの1隅に垂直方向の荷重をかけたときの薄板の曲げを計算しました。
3.1.線形モデル
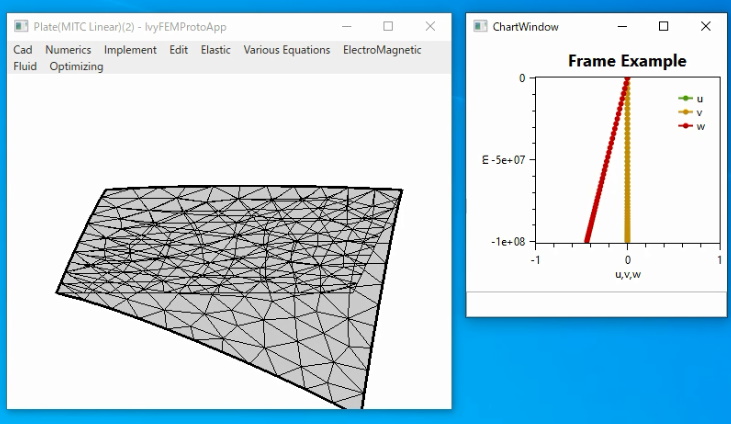

DKT要素やMindlin要素とほぼ一致しています。変位(u,v,z)-荷重(m)グラフは線形になっています。
3.2. 幾何学的非線形(St.Venant-Kirchhoffモデル)


変位-荷重グラフが期待したように非線形になっています。また線形モデルではほとんど高さ方向((z方向)の変位のみでしたが、St.Venant-Kirchhoffモデルではx,y方向変位もあることが確認できます。St.Venant-Kirchhoffモデルの方がより現実の変形を表現できていると思われます。
4. まとめ
MITC3シェル要素を用いて線形弾性体、幾何学的非線形弾性体(一例としてSt.Venant-Kirchhoffモデル)の薄板曲げを計算しました。
Mindlin板要素による薄板の曲げの計算
1. はじめに
前記事ではDiscrete Kirchhoff板理論による三角形要素(DKT要素)を使いましたが、今回はMindlin板理論による三角形要素を使って薄板の曲げを計算します。
2. 定式化

pdfにまとめました。
Reissner-Mindlin Plate Bending Triagular Elements
http://starlightparade.usamimi.info/ivyfem/doc/MindlinPlate.pdf?p=0
Mindlin板要素はせん断ロッキングが発生し、その対処として剛性マトリクスを(Timoshenko梁のように)低減積分する方法が試されました。しかし、剛性マトリクス全体を低減積分する方法では別の非物理的な解(ゼロエネルギーモード)が発生してしまうため、剛性マトリクスの横断面せん断ひずみに関してのみ低減積分を行う方法(選択的低減積分)がとられるようになりました。
3. 計算結果
3.1. 曲げの計算結果

板の寸法
a = 1.0
b = a
厚さh = 0.2a
板の材料定数
密度ρ = 2.3 x 10^+3 kg/m^3
Young率 E = 169.0 x 10^+9
Poisson比 = 0.262
せん断補正係数Ks = 5.0 / 6.0(長方形断面)
3隅を固定し、残りの1隅に垂直方向の荷重をかけたとき


3.2. 固有振動の計算
3隅を固定したとき

4隅を固定したとき

4. まとめ
Mindlin板要素を使って薄板の曲げを計算しました。DKT要素と比べると概ね同じ結果が得られました。
Discrete Kirchhoff Theory(DKT)三角形薄板要素(Flat Plate Element)による曲げの計算
1. はじめに
薄板の曲げの理論にはKirchhoffの板理論があります。ただ、この理論に基づく2次元要素に有効なものはないとのことです。
Kirchhoffの板理論を一般化したReissner-Mindlinの板理論を基礎とし、2次三角形要素の6節点上でのみKirchhoffの仮定を満たすとしたDiscrete Kirchhoff Theory(DKT)は有効な要素であることが知られています。
〇Kirchhoffの板理論
変形前中立面に垂直だった直線は変形後も直線であり、その直線は変形後の中立面に垂直である
〇Reissner-Mindlinの板理論
変形前中立面に垂直だった直線は変形後も直線であるが、その直線は変形後の中立面に垂直である必要はない
2. 定式化
pdfにまとめました。
Plate Bending Theory of Discrete Kirchhoff Triangle (DKT) Elements
http://starlightparade.usamimi.info/ivyfem/doc/DKTPlate.pdf?p=0

3. 計算結果
3.1. 曲げの計算結果

板の寸法
a = 1.0
b = a
厚さh = 0.2a
板の材料定数
密度ρ = 2.3 x 10^+3 kg/m^3
Young率 E = 169.0 x 10^+9
Poisson比 = 0.262
せん断補正係数Ks = 5.0 / 6.0(長方形断面)
3隅を固定し、残りの1隅に垂直方向の荷重をかけたとき


3.2. 固有振動(固有値問題)
3隅を固定したとき、

4隅を固定したとき、
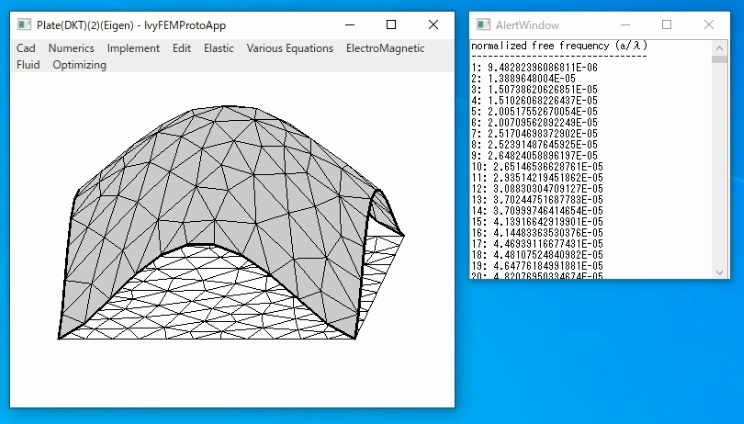
4.まとめ
Discrete Kirchhoff理論に基づく薄板三角形要素を実装し、曲げの計算を行いました。
Total Lagrange法による幾何学的非線形梁(Euler-Bernoulli field-consistent TL Beam、Timoshenko TL Beam)の計算
1. はじめに
幾何学的非線形梁をTotal Lagrange法を用いて計算します。
Euler-Bernoulli梁の場合は、変位と回転角に関係式が存在するため、変位2つ(uX、uY)と回転角(θ)は自由度について非線形な補間関数を構成する必要があります。これをfield-consistentな補間と呼んでいます。
Timoshenko梁の場合は、変位uX、uYとθは独立して補間、つまり従来のLagrange補間しても問題ないようです。
2. Total Lagrangian Beamの定式化
pdfにまとめました。
Euler-Bernoulli Field-Consistent Beam(Frame) Using Total
Lagrangian Formulation
http://starlightparade.usamimi.info/ivyfem/doc/FieldConsistentTLFrame.pdf?p=0
Timoshenko Beam(Frame) Using Total Lagrangian Formulation
http://starlightparade.usamimi.info/ivyfem/doc/TimoshenkoTLFrame.pdf?p=0
3. 片持ち梁の計算結果
梁
長さL = 1m
幅b = 0.2L
高さh = 0.25b
梁の物性値
密度ρ = 2.3e+3 kg
Young率 E = 169.0e+9
Poisson ν= 0.262
とします。
FはY方向荷重で、上方向を+とします。
以下の結果のグラフでuはX方向(水平方向)変位、vはY方向(垂直方向)変位です。
mは断面換算の荷重で、断面積A(=bh)として、
m = F A = F (bh) [kg m^2]
としています。

3.1. Euler-Bernoulli field-consistent Beam


3.2. Timoshenko Beam
shear locking回避のため剛性行列の計算には低減積分を用います。


4. まとめ
幾何学的非線形な梁を扱うためにTotal Lagrange法を導入しました。
Euler-Bernoulli梁の場合は、field-consistentな補間関数を構成する必要性が分かりました。Timoshenko梁の場合は、従来の補間関数を用いることができることを確認しました。
Co-rotational Beam(Frame):Euler-Bernoulli Shallow Arch BeamとTimoshenko Beam
1. はじめに
幾何学的非線形な梁をCo-rotational法を用いて計算しています。
Co-rotational法は変位を剛体運動と微小変形に分離して考えます。

Euler-Bernoulli Shallow Arch梁とTimoshenko梁について定式化しています。
2. Co-rotational Formulation
pdfにまとめました。
Co-rotational Beam(Frame) Formulation
http://starlightparade.usamimi.info/ivyfem/doc/CorotationalFrame.pdf?p=0
Timoshenko Co-rotational Beam(Frame) Formulation
http://starlightparade.usamimi.info/ivyfem/doc/TimoshenkoCorotationalFrame.pdf?p=0
3. 片持ち梁の計算結果
梁
長さL = 1m
幅b = 0.2L
高さh = 0.25b
梁の物性値
密度ρ = 2.3e+3 kg
Young率 E = 169.0e+9
Poisson ν= 0.262
とします。
FはY方向荷重で、上方向を+とします。
以下の結果のグラフでuはX方向(水平方向)変位、vはY方向(垂直方向)変位です。
mは断面換算の荷重で、断面積A(=bh)として、
m = F A = F (bh) [kg m^2]
としています。

3.1. Euler-Bernoulli (Shallow Arch) Corotational Beam


3.2. Timoshenko Corotational Beam
shear locking回避のために剛性行列の計算には低減積分を用います。


4. 比較:微小変形梁理論の計算結果
Co-rotational法と比較するため微小変形の梁について計算しました。
Co-rotationalでは回転を表現できていましたが、微小変形梁理論では変形が線形となって回転を表現できていないようです。
4.1. Euler-Bernoulli Beam


4.2. Timoshenko Beam


5. まとめ
幾何学的非線形な梁を計算するためにCo-rotationalな定式化を行い、片持ち梁を計算しました。
ビーム(フレーム)要素をトラスに適用するとき回転角の扱い
1. はじめに
フレーム要素を下記のような梁+トラス構造の解析に使いましたが、間違っていることに気付いたので記します。

2. 複数のビームが接続する節点の連続性
3つのビームが1つの節点に接続されている場合、X方向変位u、Y方向変位vは連続としていいのですが、回転角θ(ビームの傾きの変位)は連続ではないことが分かります。
u1=u2=u3=u
v1=v2=v3=v
θ1 != θ2、θ1 != θ3、θ2 != θ3
この節点に何の条件も課さないとθを連続としたことになるため、不合理が生じます。

3. トラス付き梁の計算結果
トラスの接続節点ではすべて回転角θ = 0という条件を課して再計算しました。
3.1.Euler-Bernoulli梁


3.2.Timoshenko梁


4. まとめ
トラスのような3つ以上の梁が1点に接続されている場合や、梁の方向が不連続に変化する場合は回転角が不連続になるのでなんらかの条件を考慮する必要があると思われます。トラスの場合は回転角を0とする条件を用いました。